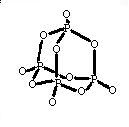
Ækvivalentvægt1 med hensyn til en komponent.

JJ/11.00

Sumformlen eller den empiriske formel for et rent stof angiver udelukkende det relative forhold mellem de atomer, som stoffet er opbygget af. Molekylformlen afspejler hvilken mindste del af stoffet, der stadig har dets kemiske egenskaber. Strukturformlen for et stof indeholder information om den rumlige opbygning. At finde sumformlen for et rent stof ud fra analytiske data er en mellemstation til (en forudsætning for) at kunne beskrive stoffets opbygning.

EX. Empirisk formel: P2O5

Molekylformel: P4O10

Strukturformel:

Støkoimetrien (altså de relative molforhold) i kemiske reaktioner beskrives ved hjælp af afstemte reaktionsskemaer og kan under anvendelse af molbegrebet oversættes til makroskopisk afmålelige mængder stof. EX1 Afbrændingen af fosfor i ren oxygen giver fosforpentaoxid.

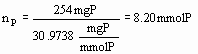
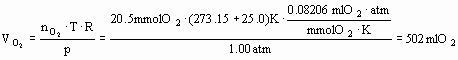
2P + 5O2 ® P2O5. Det betyder, at reaktionens støkiometri er givet ved: , hvor n står for stofmængden regnet i enheden mol. Er der fx anvendt 254 mg fosfor er det


(bemærk: 3 betydende cifre på trods af at MP kendes mere nøjagtigt.)
Til 8.20 mmol P går der et antal mmol O2 svarende til det støkiometriske forhold: ,
hvilket svarer til et vist volumen ren oxygengas ved 25 0C og 1 atm:

Bemærk: i størrelsesligningen indsættes tal og enheder, som hver især ganges og forkortes efter regneforskriften. Specielt er den enhed der kommer ud af det hele en kontrol på at størrelsesligningen (altså regneforskriften) er rimelig.

De rå analytiske data er resultatet af eksperimenter, som kan være af flere tilsnit.
Fælles for de fleste er imidlertid, at der benyttes en metode, som kan afsløre en stofmængde nA af en komponent A i en masse-portion mU af det analyserede rene stof U. Det relative forhold mellem disse to størrelser er nyttig og kaldes ækvivalentvægten UÆA af det rene stof U med hensyn til komponenten A. UÆA = mU/nA. Enheden er gU/molA.

EX1(fortsat) I et rent stof U hvori der kun er fundet P og O er der fundet 3.33 mmol P i en portion på 236 mg U.

UÆP = 236·mgU/3.33,mmolP = (70.87xx=70.9)·gU/molP.

Bemærk 1: 3 betydende cifre i massen og stofmængden og derfor også i resultatet.

Bemærk 2: En størrelse kan betragtes som produktet af et tal og en enhed.

70.9 g U indeholder altså netop 1 mol P med MP = 30.9738·gP/molP. Resten er oxygen . U har sumformlen POx og vejer pr. mol det samme som UÆP : UÆP·(nP/nPox) = MP·(nP/nPox) + MO·(nO/nPox) eller

70.9· (gPOx/molP)·1·(molP/molPOx) = 30.9738·(gP/molP)·1·(molP/molPOx) + 15.999·(gO/molO)·x·(molO/molPOx).

Heraf findes x til 2.50 (rent tal). Sumformler angives sædvanligvis med hele tal, så den empiriske formel for U er her fundet til P2O5.

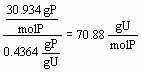
 I visse tilfælde kan man stå med andres bearbejdede analytiske data for indholdet af en komponent, formuleret som masse%, dvs hvor mange g af komponenten A findes der i 100 g af stoffet U. Sådanne tal kan omsættes til ækvivalentvægten af det rene stof U med hensyn til komponenten A. EX1(fortsat) Et stof U oplyses at indeholde 43.64% P, medens resten er oxygen. Sumformel POx . MP= 30.934gP/molP .

Videre gælder at 70.88 = 30.934 +x·15.9994, hvoraf x = 2.500. Da sumformler indeholder hele tal skrives sumformlen ikke PO2.5 , men som P2O5

 

De fleste beregninger må forholde sig til hvordan de analytiske data er opnået.

Masse-portionen mU af det analyserede rene stof U bestemmes ved vejning.

Stofmængde nA af komponenten A kan bestemmes ved hjælp af forskellige metoder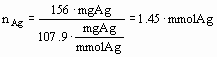
1. Ved vejning af en bestemt kemisk forbindelse, som indeholder komponenten A og som er isoleret via en kendt kemisk reaktion udført på portionen mU af stoffet U.

EX2: Ved elektrolyse på en opløsning af en portion på 246 mg af et stof U, hvori der er identificeret sølvioner og ikke andre metaller, er der afsat netop 156mg sølv på platinkatoden.


som fandtes i 246 mg U. Ækvivalentvægten UÆAg af det rene stof U med hensyn til Ag er da

Resultat med tre betydende cifre.

(Tallene er konstruerede med stoffet sølvnitrat med M=169.873g/mol i tankerne)

EX2(fortsat) Ved at fælde med overskud af saltsyre på en portion på 246 mg af et stof U, hvori der er identificeret sølvioner og ikke andre metaller, er det ved vejning konstateret at der er dannet netop 208 mg sølvchlorid.


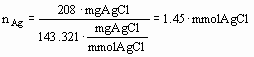
Da der er 1 mol Ag pr mol AgCl, er der 1.45 mmol Ag i portionen på 246 mg U og ækvivalentvægten findes som ovenfor (det var også sølvnitrat).

 2. Ved titrering af en opløsning af portionen mU af stoffet U til ækvivalenspunktet (til omslag) med et vist volumen vx af et reagens x i opløsning og med koncentrationen Cx M, idet det af et afstemt reaktionsskema fremgår at f·nA = nx som jo er vx·Cx . Det betyder at nA = (vx·Cx)/f

EX2(fortsat) En opløsning af en portion på 246 mg af et stof U, hvori der er identificeret sølvioner og ikke andre metaller, titreres til rødfarvning med netop 14.5 ml 0.100 M kaliumchlorid-opløsning med kaliumchromat som indikator. nAg = {(14.5·0.100)/1 = 1.45}mmol. (Stoffet U er det samme som før ).

 3. Ved at tilsætte en kendt mængde af et reagens y (fx vy ml Cy M, som er overskud) til en (evt. kemisk modificeret) portionen mU af stoffet U og derefter titrere tilbage med vz af et reagens z med en koncentration Cz . Af afstemte reaktionsskemaer fremgår det, at y og A reagerer i et forhold, så fA·n'A = n'y og at y og z reagerer i et forhold, så fz·n*z = n*y . Når nu ny = fz·nz + fA·nA fås, at nA = (ny - fz·nz )/fA = (vy·Cy - fz·vz·Cz)/fA , det hele regnet i mmol, når v'erne regnes i ml.

EX2(fortsat) Ved at reducere en opløsning af en portion på 246 mg af et stof U, hvori der er identificeret nitrat med et overskud af zink og svovlsyre dannes der en ækvivalent mængde ammoniumioner; nammonium = nnitrat = nN. Efter at have tilsat et godt overskud af stærk natriumhydroxid koges blandingen og destillatet (med ammoniak) opsamles i 12.50 ml 0.100M svovlsyre. Der titreres herefter tilbage med 10.5 ml 0.100M NaOH med methylrødt som indikator ( rød til gul). Af reaktionsskemaer fremgår at der går 2mol ammoniak til 1 mol svovlsyre og at der går 2 mol natriumhydroxid til 1 mol svovlsyre. nN = (nsvovlsyre - ½·nnatriumhydroxid)/½ ={2·(12.50·0.100 - ½·10.5·0.100) = 1.45}mmol N. (U er stadig sølvnitrat) Bemærkning. Normalt opsamles ammoniak i saltsyre i standard Kjeldahl analyse. Her er anvendt svovlsyre kun for at også at illustrere beregningen, når reaktionerne ikke foregår i molforholdet 1 til 1.

Flere analyser på samme stof U er basis for at kunne bestemme sumformlen for U. Dels giver de fundne ækvivalentvægte med hensyn til forskellige komponenter direkte det støkiometriske forhold mellem komponenterne. I tilgift ligger der den oplysning i de beregnede ækvivalentvægte om de fundne komponenter er de eneste komponenter i det rene stof.

EX2(fortsat) I det stof U, hvor der var fundet sølvioner (og ikke andre metaller) og nitrationer, har vi de to ækvivalentvægte som er bestemt ud fra uafhængige analysemetoder:

UÆAg = 170gU/mol Ag og UÆN = 170gN/mol N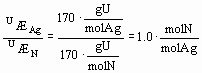

Forholdet mellem dem er vigtigt , selvom det i dette tilfælde er ret trivielt.

Udregningen viser at i stoffet U er forholdet mellem sølvioner og nitrationer 1 til 1, hvilket passer med forventningerne, idet anionen ladning på -1 og kationens ladning på +1 i et rent stof må forekomme i lige store mængder fordi U (som alle andre rene stoffer) ikke kan have nogen nettoladning.

Nu til spørgsmålet om stoffet er rent eller evt. indeholder en neutral komponent. At der i faste rene salte er budnet et antal vandmolekyler i krystalgitteret er hyppigt forekommende. Den største af de fundne ækvivalentvægte indeholder netop 1 mol af den sjældneste komponent (den med de laveste tal - 1 - i sumfomlen). Denne værdi må så også være sumformlens molarmasse. Og det kan bruges til at beregne om de fundne komponenter i det fundne forhold er alene i stoffet.

EX2(fortsat) Antager vi at vores stof U er rent, så kunne det jo indeholde krystalvand og have sumformlen

AgNO3 ,xH2O. Dette stof har molarmassen MAg + MN + 3·MO + x·Mvand

og værdien er fundet til 170 g/mol. Heraf kan x bestemmes til (170 - 108 - 14 - 48)/18 som er = 0.
U er med andre ord sølvnitrat, AgNO3, og indeholder altså ikke krystalvand.