
figur 1
Madelung konstanten.
Gitterenergien af et mol af et krystallinsk salt kan jo opfattes som den energi der vindes ved at forene et mol af hver af de involverede ioner ved at overføre dem fra en tilstand, hvor de er fuldstændigt separerede fra hinanden (de gasformige enkeltioner) til en tilstand hvor de er placerede i gitteret i en perfekt krystal. Det svarer så omvendt til at tage et mol krystal og tilføre gitterenergien, så der opnås et mol gasformige ioner.
Ioner vekselvirker især ved elektrostatiske kræfter, hvor Coulombs lov fortæller, at tiltrækningskraften er proportional med hver af ladningernes størrelse og omvendt proportionalt med afstanden mellem ladningerne i anden potens. Kraften regnes positiv, når ladningerne har forskelligt fortegn. Den tilsvarende energi er omvendt proportionalt med afstanden.
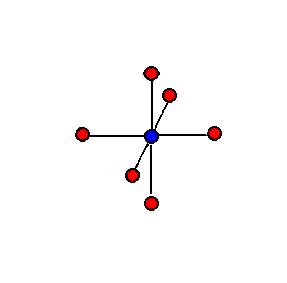
Der er netop 6 kugler i af standen a og disse 6 kugler giver en samlet tiltrækning på 6 gange ![]() . Princippet er videre, at vi hitter de næst nærmeste naboer med ens afstand, som hver især bidrager med samme tiltrækning eller frastødning. Fortegn, afstand og antal er derfor de faktorer der skal føjes til det generelle Coulomb udtryk. Summen af alle disse faktorer på et og samme Coulomb udtryk er med andre ord kun afhængig af geometrien i opbygningen af saltet og kaldes Madelung konstanten for den pågældende type krystalopbygning.
. Princippet er videre, at vi hitter de næst nærmeste naboer med ens afstand, som hver især bidrager med samme tiltrækning eller frastødning. Fortegn, afstand og antal er derfor de faktorer der skal føjes til det generelle Coulomb udtryk. Summen af alle disse faktorer på et og samme Coulomb udtryk er med andre ord kun afhængig af geometrien i opbygningen af saltet og kaldes Madelung konstanten for den pågældende type krystalopbygning.
Med de 3x3x3 = 27 kugler (figur 1) ser regnskabet sådan ud.
I afstanden 1 a er der 6 røde kugler - svarende til tiltrækning. Faktoren på Coulomb udtrykket er da ![]() . (figur 2)
. (figur 2)
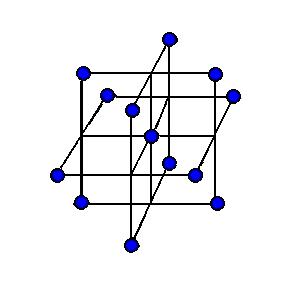
I afstanden Ö2 a er der 12 blå kugler - svarende til frastødning. Faktoren på Coulomb udtrykket er da ![]() . (figur 3)
. (figur 3)
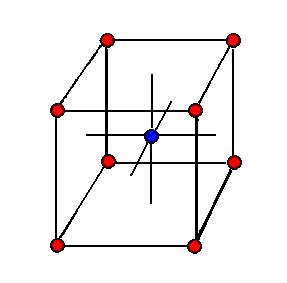
I afstanden Ö3 a er der 8 røde kugler - svarende til tiltrækning. Faktoren på Coulomb udtrykket er da ![]() . (figur 4).
. (figur 4).
De tre led skal lægges sammen efter at være korrigeret for den ladning der er i en enhed der kun omfatter de 27 kugler. De første 6 kugler (jf. figur 2) på fladerne er i en hel krystal fælles for to flader og dermed for to sæt af 27 kugler sat ved siden af hinanden. Deres ladning skal derfor hver regnes med i 2 ens sæt af 27 kugler og derfor kun halv i hvert af de to sæt. Det første led bliver derfor ![]() .
.
Tilsvarende er hver af de 12 blå kugler (figur 3) på kanterne fælles for 4 ens sæt af 27 kugler og ladningen skal derfor kun regnes med ![]() gange. Det andet led bliver derfor
gange. Det andet led bliver derfor ![]() .
.
Tilsidst er hver af de 8 røde kugler (figur 4) i hjørnerne fælles for 8 ens sæt af 27 kugler og ladningen skal derfor kun regnes med ![]() gange. Det andet led bliver derfor
gange. Det andet led bliver derfor ![]() .
.
Summen af disse tre ladningskorrigerede led er -1.456. 1.456 er da første tilnærmelse til Madelung konstanten .
I næste tilnærmelse kan vi betragte 5x5x5 = 125 kugler. I dette tilfælde hører alle de 27 kugler i første tilnærmelse med til "inderkredsen" og disses ladningerne skal i denne tilnærmelse medregnes fuldt ud, hvorimod de ydere 98 kugler skal regnes med som halve (de 6x9=54 på fladerne), som fjerdedele (de 12x3=36 på kanterne) og som ottendedele (de 8 i hjørnerne). Madelung konstanten i denne tilnærmelse bliver 1.752.
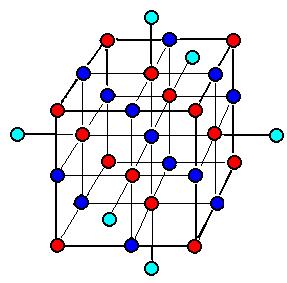
På ovenstående figur er 1 natriumkerne angivet midt i det nye, yderste lag angivet med en lidt anden blå farve. Deres afstand er netop 2a.
Tager man et større og større antal gitterpunkter konvergerer tallet mod 1.748 (4 betydende cifre), så allerede 125 gitterpunkter giver en korrekt værdi til 3 betydende cifre (1.75).
Madelung konstanten er den af gittertypen afhængige geometriske faktor der skal ganges på Coulomb-udtrykket. Den kan regnes ud for alle mulige gittertyper. For CsCl strukturen (8:8 - BCC) er den 1.763.