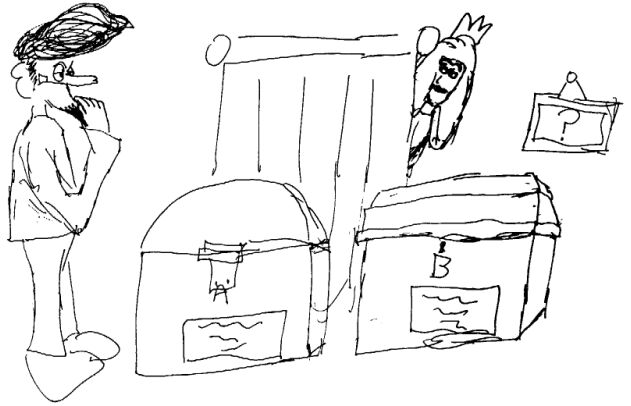
Mit yndlingsparadoks: Portias portræt
Af Peder Voetmann Christiansen.Hvis ikke man interesserer sig for paradokser, er man sandelig, som Kierkegaard siger, "en mådelig patron". Det har jeg lagt mig på sinde, og i mange timer svimlet skadefro over Russell's "mængden af alle mængder, der ikke er element i sig selv" eller Richards "det mindste hele positive tal, der ikke kan defineres med tolv ord" (tæl selv efter). Disse såkaldt syntaktiske paradokser, der på et rent sprogligt plan, uden reference til nogen ikke-sproglig virkelighed lægger en bombe under formalismeberuste matematikeres tro på, at de frit kan opfinde begreber som luftkasteller, der ikke hviler på nogen praksis ud over dyrkelsen af den rene matematik. På en måde er det nemt at komme sig oven på chokket fra et af de syntaktiske paradokser. Man kan jo blot slå sig til tåls med, at sådanne rent sproglige konstruktioner ikke har noget med noget at gøre. Men så er man moden til at konfronteres et af de semantiske paradokser, der griber ind til kernen af sprogets væsen, nemlig at det gerne skulle handle om noget. En sætning skal kunne fortolkes og sættes i relation til nogle fakta, så man kan afgøre, om den er sand eller falsk. Et semantisk paradoks vil ofte indeholde ord som "sand" eller "falsk" eller "lyver" i forbindelse med en direkte eller indirekte selvreference. Det mest velkendte eksempel er nok løgnerparadokset "denne sætning er ikke sand".
At forbyde selvreference løser ikke problemet. Det ville være som at smide barnet ud med badevandet, for hele sproget hviler jo på en indviklet og ofte uigennemskuelig visen tilbage til sig selv. Tænk bare på en ordbog, hvor alle ord i et givet sprog forklares med andre ord fra samme sprog. Det udelukker jo som bekendt ikke, at sproget kan handle om noget andet end sig selv; måske er det ligefrem en nødvendig forudsætning for, at det kan lade sig gøre. Men sætninger, der bare handler om sig selv eller om andre sætninger, der blot viser tilbage til den første, uden at der optræder den mindste henvisning til en virkelighed uden for sproget, virker alligevel lidt tandløse i deres paradoksalitet. Det er jo ikke den slags sætninger, vi går rundt og bruger til daglig. Hvis man ikke er matematiker eller logiker kan man ikke for alvor blive rystet over en leg med ord, der slet ikke involverer "den virkelige virkelighed". Derfor har jeg i årevis benyttet den følgende historie om Portias portræt i foredrag, der handler om forholdet mellem sprog og virkelighed, bl.a. som det viser sig i kvantefysikkens grundlagsproblemer. Hvis der skulle være nogen af mine tidligere tilhørere blandt læserne, beder jeg dem undskylde min monomane gentagelsestrang: jeg kan simpelt hen ikke blive færdig med den. Historien findes i Shakespeares "Købmanden i Venedig". Matematikeren Raymond Smullyan har parafraseret den på forskellige måder i sin herlige bog "What's the Name of This Book?", og en af disse versioner har jeg udvalgt og pyntet lidt mere på. Her kommer den: Prinsesse Portia, en meget sofistikeret kongedatter, vil gerne giftes, men ikke med hvem som helst. Derfor udskriver hun en bejlerkonkurrence: Den første mandsperson, der løser et givet problem, vil hun gifte sig med; men hvis han ikke løser det, vil han blive straffet. Der melder sig kun én bejler, en logikprofessor fra byens universitet.
Portia fører ham n ind i et rum, hvor der står to skrin. Hun siger: "Mit portræt ligger i et af disse to skrin. Hvis du åbner det rigtige skrin og finder portrættet, sk l vi giftes, ellers - -". Bejleren ser på skrinene og bemærker, at der er et påskrevet skilt på hvert af dem. På det ene (skrin A) står der:
A
Portrættet ligger i det andet skrin.og på det andet (skrin B) står der:
B
Et og kun ét af disse to skilte lyver.Nu begynder han at anvende den logik, han er ekspert i, og ræsonnerer som følger:
"Sætningen på skrin A er enten sand eller falsk, men hvis jeg skal afgøre det, må jeg åbne et af skrinene, og så er der 50% chance for, at det er det forkerte, og at jeg får hovedet hugget af, så det tør jeg ikke risikere. Men måske kan jeg bruge sætningen på skrin B. Lad os se - - hvis den er sand, så er der altså netop ét af de to skilte, der lyver, og det må jo så være det på skrin A. Så må portrættet være i skrin A. På den anden side, hvis skilt B lyver, så er det altså ikke rigtigt, at netop et af skiltene lyver. Det må så betyde, at de begge lyver, og så må portrættet være i skrin A. Sagen er klar, for begge antagelser fører til den samme konklusion."
Så går han triumferende hen og åbner skrin A, men det er tomt! I det samme lyder en fnisen bag forhænget, og Portia dukker frem. Rystet anklager han hende for at have brudt spillets regler, men hun går roligt hen og åbner skrin B, og d‚r ligger portrættet. Historien slutter med, at hun giftede sig med ham. Denne uheldige (men i sidste instans heldige) bejler har oplevet et virkeligt paradoks, men læg mærke til, at hvis portrættet havde været i skrin A, havde der ikke været noget paradoks. Den virkelige virkelighed har her et afgørende ord at skulle have sagt. Bejlerens tillærte logiske tænkning kom til kort, og det har givet ham noget at tænke over. Portias "kvindelige" logik er af en anden art, men den er ganske klar: Hun har lokket ham i en fælde, som var specielt indrettet til at fange en logiker. Når han således er sat på plads, ‚n gang for alle, kan hun roligt gifte sig med ham.
Anklagen om at have snydt kan hun tage ganske roligt; hun havde jo ikke sagt et ord om, at skiltene på skrinene havde noget med portrættets beliggenhed at gøre. På den anden side: skiltet på skrin A har en klar betydning, og den besked, det giver, er faktisk sand. Skiltet på B giver derimod en besked uden klar forbindelse med fakta, den er uhjælpeligt vag (som Peirce ville have sagt). Hvis portrættet havde været i A, som han troede, kunne den have været betragtet som både sand og falsk, uden at det ville gøre nogen forskel. Sådan som sagen faktisk forholder sig, kan den hverken være sand eller falsk, uden at det fører til en modstrid. Hvis han havde vist lidt mere sund sans og bygget på den tillid til sandheden af en klar besked, som er så gavnlig, ikke mindst i et ægteskabeligt forhold, ville han ikke have snydt sig selv.
Vi må altså se i øjnene, at hvis vi vil tænke logisk på en forpligtende måde, således at vi anerkender, at sætningerne handler om noget virkeligt, dvs. noget, der eksisterer uafhængigt af vore fordomme, så er der ikke noget system for tænkning, der er ufejlbarligt. Det er vi tilbøjelige til at glemme, og derfor har vi brug for paradokset.
Tegning af Harald Voetmann ChristiansenReferencer
- Fraenkel and Bar-Hillel, Foundations of Set Theory, North Holland, Amsterdam, 1958. (Om matematiske paradokser eller antinomier, Russell, Cantor, etc.)
- Shakespeare, Købmanden i Venedig, Akt 2, scene 7.
- Smullyan, What's the Name of This Book ?, Englewood Cliffs, N. J.: Prentice Hall, 1978.
- Claudine Engel-Tiercelin, Peirce's Logic of Vagueness, Tekster fra IMFUFA, RUC, 1991.
Tilbage til Peder Voetmann Christiansens hjemmeside