Peircean local realism does not imply Bell's inequalities.
Extended abstract for a paper submitted to the "Symposium on the Foundations of Modern Physics", Joensuu, august 1990. The paper following the abstract consists in part of material from a poster presented at the symposium. The last part was developed in a dialogue with A. Zeilinger.
Peder Voetmann Christiansen
Department of Mathematics and Physics (IMFUFA)
Roskilde University (RUC)
DK 4000 Roskilde
Abstract
The concept of "local realism", also called "local causality" or "Einstein locality"
was introduced in connection with the famous 1935-paper by Einstein, Podolsky and
Rosen with the purpose of indicating a fundamental incompleteness of the quantum
mechanical formalism. Later, Bell connected the concept with the existence of "local
hidden variables" and was able to show that the existence of such quantities lead to
inequalities concerning correlations of spins or polarizations of a particle pair, and that
these inequalities sometimes are violated by quantum mechanics. A considerable number
of sophisticated experiments, mainly Aspect's in 1982, have subsequently shown that
quantum
mechanics gives the correct predictions under such circumstances, and that the
Bell-inequalities are violated. Still some small "loopholes" exist, but the conclusion seems
reasonably clear: The concept of local realism that is connected with the existence of
local hidden variables is incompatible with the experiments.This conclusion is then in many cases regarded as evidence for non-locality of the quantum mechanical formalism. It is the purpose of this paper to point out that this needs not be the case. As regards practical consequences of the presumed non-locality, such as possibilities for sending superluminal signals they seem to be non-existing. From a pragmatic point of view it therefore seems less than satisfactory to adopt a philosophical interpretation of the formalism that allows non-locality even a "ghost-like" existence. This problem can be avoided if it can be demonstrated that the broader concept of local realism, as needed in the Einstein-Podolsky-Rosen argumentation is not equivalent with Bell's idea of local hidden variables.
Indeed, there exists a more general conception of local realism that can be mathematically formalized and is compatible with the quantum mechanical formalism. The so called "synechistic" philosophy which occupied a considerable part of C.S.Peirce's thinking from 1892 to his death in 1914 lives up to these specifications. Unfortunately, Peirce's synechism has been virtually unknown by the pioneers of quantum philosophy due to the late and insufficient publication of his papers. Moreover, some of the editors of Peirce's work have been too quick to express the opinion that that the Peircean philosophy of continuity (i.e. synechism) is unable to grasp the essential discreteness of quantum physics. This paper will show that the discreteness of the transition from potentiality to actuality connected with the collapse of the wave function is well described in peircean semiotic as a transition between the sign categories index and symbol. An index cannot in general be represented numerically and the indexical character of quantum mechanical state vectors is, therefore, not compatible with the notion of hidden variables. There is no difficulty in regarding Dirac's quantum formalism as an instance of Peircean semiotic and the locality and continuity expressed by the partial differential wave equations corresponds well with Peircean synechism.
A consequence of the Peircean view of state vectors as indices is that numerical properties of quantum systems are always contextual, i.e. they exist only in connection with well defined setups of measuring apparatuses. A property of a pair of particles may therefore be expected to depend on whether there exist a common context for the measurements on the single particles, or not. Following this line of thought it is possible to construct a classical scenario where every interaction is strictly local, but where Bell's inequalities are clearly violated. The example can be formulated as an interview where a sociologist ask a couple of "twins" about their political affiliations, but where the truth of the answers depends on certain "signals" emitted by the sociologist. It turns out that Bell's inequalities may be violated if the twins are interviewed by the same sociologist, but never with two different sociologists.
Although the example has no direct connection with quantum mechanics and Aspect's experiments it suggests some points that may be worth investigating. The coin- cidence counters used in the experiments look like a common context for the polarization measurements of the two photons in a cascade pair, so it may be suggested that a similar experiment performed with truly independent measurements on the two particles may conform with Bell's inequalities. This point can only be investigated experimentally. A philosophical point that can be made on the basis of the example, or Peircean synechism in general, is that there is no need to look for more or less extravagant ontological speculations, like splitting universes, backwards causality, or superluminal signals in order to justify the consistency and relative completeness of the quantum formalism.
Continuity versus discreteness
"I find something pathetic in Peirce's failure to anticipate both basic aspects of quantum physics, instead of only one of them (indeterminism), for he had all the conceptual tools needed for the second anticipation (discontinuity). Moreover, indicating the right direction for the development of physics was one of his professed ambitions and, he thought, a test for the soundness of his philosophy." (Hartshorne (note 2), quoted from Fernandez (note 3)).Hartshorne seems to have overlooked that synechism also treats the concept of discreteness, or discontinuity as a necessary ingredient in the continuum. Indeed, in several discussions of mathematics that were omitted in the "Collected Papers" by Hartshorne but later included in the "New Elements of Mathematics" (NEM) collected by Carolyn Eisele (note 4), Peirce draws attention to the topological invariants of space (the Listing numbers, NEM III.112) as a class of non-relative properties that precede the continuity properties. Moreover, in his triadic system of categories continuity is described as a "thirdness" whereas discreteness is a "secondness". This corresponds with the semiotic classification of the signs that point to distinguishable objects, indices, as secondary or dyadic signs whereas continuous numerical properties are described as full triadic signs depending on an interpretant, i.e. symbols, whose meaning is only defined in the context of statistical uncertainties arising from the experimental situation.
According to Peirce a sign is an irreducible triadic relation between 1. a sign vehicle, 2. an object, and 3. an interpretant. A full-fledged triadic sign is called a symbol. However, there exist "degenerate" types of signs where one or more of the factors in the sign relation are latent. Thus, in the absence of an interpretant the sign degenerates to a dyadic type called an index, and if also the object is latent (or "in the shadow" of the sign vehicle) we have a monadic sign called an icon.
In quantum mechanics we find a clear example of the use of these three categories of signs. Thus, the basic notion of a particle is an icon, its state vector without regard to any representation is an index, and its numerically measurable properties, given by matrix elements of certain operators in a representation determined by the ex- perimental context, can be classified as symbols. The setting of an interpretant is a discrete topological transformation of the sign relation, and therefore discreteness is somehow inherent in the quantum formalism. The quantum jump described as "the collapse of the wave function" can be regarded as a discrete transition from a potential symbolic property to an actual one, and this type of discrete jump is therefore of a topological nature in connection with the very nature of the sign relation. Another type of discreteness in quantum mechanics is connected with the eigenvalue spectrum of the operators representing observables of bounded systems. This is explained in wave mechanics as due to the finite value of the quantum of action and therefore not directly related to Peirce's semiotic. However, as the operators are defined on a continuous space, nothing contradicts synechism.
Derivation of Bell's inequalities and Fine's theorem
The derivation of Bell's inequalities from classical probabilistic logic seems to suffer from
the supposition that joint distributions exist for properties like a1
and b1 that are incompatible according to quantum mechanics.
Consider the following derivation where we disregard all questions of incompatibility.
The whole probability space can then be divided into 16 subsets of the 4 properties
a1, b1, a2,
and b2. In the table below these subsets are indicated in a
binary notation in the leftmost four columns. To the right other four columns show with
an x if a certain subset belong to one of the four separation sets
S(a1,a2),
S(a1,b2),
S(b1,a2), and
S(b1,b2). Finally, in the rightmost
column a number shows how many times a subset counts in the sum
S = S(a1,a2) + S(a1,b2) + S(b1,a2) - S(b1,b2)
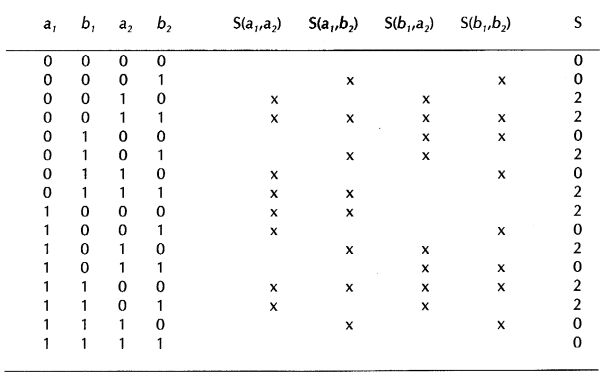
It is seen that each of the subsets counts either twice or nothing to the sum S, and as the total probability measure of all the subsets adds to unity, the value of S must lie between 0 and 2, which is equivalent to Bell's inequalities (note 5,7).
The original derivation of the inequalities did not assume the existence of joint distributions for incompatible properties, but instead it assumed the existence of local hidden variables with distributions independent of the experimental setup. In 1982 it was shown by A. Fine (note 8) that the assumptions are equivalent: if Bell's inequalities are valid joint distributions of all combinations of properties will exist, at least in a mathematical sense. The assumption of local hidden variables is therefore unnecessary, and the whole derivation of the inequalities can be regarded as an application of classical probabilistic logic, as has been done in the preceding paragraphs. In connection with his theorem Fine raised the question whether the observed violations of the inequalities had been misinterpreted when it was considered a sign of an inherent non-locality in nature. What they really are about is rather the existence of joint distributions that are forbidden by quantum mechanics, says Fine. This remark may then be taken as a justification for the common view among the adherents of the Copenhagen interpretation, that there is no reason at all to be concerned about the presumed non-locality. Another conception, which is more in accordance with Peirce's local realism, is that the violation of classical logic is due to contextuality. Shimony (note 9) has presented a contextual hidden variable theory where he argues that Fine's joint distribution of incompatible properties is unphysical because no experimental context exists for their measurement. This is true, but contextuality needs no hidden variables! (note 10)
A classical scenario
In the country "Smullyana"(note 13) there are three clubs, A, B and C. Every inhabitant is a
member of at least one of the clubs, and no one is a member of more than two. The
following figure shows exactly how the population is divided among the clubs.
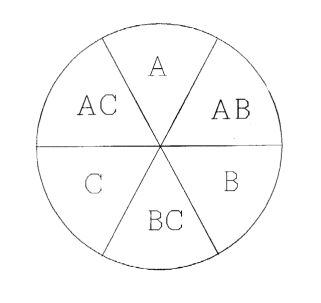
In Smullyana there are many pairs of twins, and the two members of such a pair always belong to the same club or clubs. If an "objective" sociologist picks a random pair of twins and asks each of the two persons if he or she is a member of a certain club, the probability of getting the answer "yes" is 1/2 (see fig. 3), at least if the persons answer truthfully. If the two twins are asked separately, not necessarily the same question, and if both answer "yes" the sociologist will report a "coincidence" to his institute. If now the objective sociologist asks twin 1 if he is a member of club A and twin 2 if he is a member of club B, and both twins answer truthfully, then the probability of getting a coincidence (two "yes"es) will be exactly 1/6 (see fig. 3). This is an example of how classical context-free logic can get us to the lower limit of Bell's inequality (Mermin's version), but not below. Let us now introduce contextuality in order to get below the lower limit of 1/6 probability of coincidence when two different questions are asked.
We now assume that the three clubs have an established non-transitive order of verbal attacks, such that
club A always attacks club B,We further assume that a certain fraction, q, of the twins are dishonest such that they will not answer truthfully when asked if they are members of a club they really belong to, if they know that the person asking the question belongs to the club that always attacks their own club, and they will always answer "yes" when asked if they are member of the club that attacks the sociologist's club. The sociologists (not being aware of this fact) choose to expose their own membership of one of the clubs by wearing a T-shirt with its letter clearly printed, but the sociological institute prefers to conduct its investigation of twin-memberships in such a way that a sociologist never is allowed to ask about membership in the club whose letter he is wearing himself. Assuming that the sociologists are equally distributed in the clubs the institute decides who may pose a certain pair of questions by random choice among the suitable coworkers.
club B always attacks club C, and
club C always attacks club A.
If for example the pair of questions is "A?/A?" it may be asked by B- or C-sociologists, whereas if it is "A?/B?" it may only be asked by C-sociologists, assuming that the same sociologist asks both members of the pair.
If now an A-twin is asked by a C-sociologist, if he is a member of club A, he will not answer truthfully, if he belongs to the dishonest part of the population. He will not know what question his twin brother is asked (it might be A? or B?), but he is seduced by the context (the T-shirt of the sociologist) to deviate from truth. If twins are assumed to share the property of being dishonest or not, and the other (dishonest) twin is asked B? he will answer "yes", but the probability of a coincidence has been diminished by the common context.
One finds that the probability of a coincidence for two different questions is pd = (1-q)/6, whereas that for the same question (averaged over the different possible sociologists) still is 1/2.
The coincidence sum is 3pd - ps = -q/2, below the lower limit according to Bell.
That the violation of Bell's inequality is due to a common context is illustrated by the same example if one modifies the rule such that it is always two different sociologists that ask the two questions to the separate members of a pair of twins. The two questioners are supposed to be picked at random among the suitable members of the institute. In this case one finds that the occurrence of fearful twins adds to the probability of coincidence for two different questions, such that it becomes 1/6 + q/12. So in this case Bell's inequality is satisfied, which is to be expected when the two contexts are statistically independent. It's a bit more complicated in this case, because the probability of coincidence for the same question (e.g. A?/A?) is reduced to ps = 1/2 - q/4 whereas that for different questions is increased to pd = 1/6 + q/12.
So,
3pd - ps = q/2in accordance with Bell and Mermin.0
Although the scenario is highly artificial it should illustrate that violation of Bell's inequality can occur in the absence of quantum effects or any sort of non-locality. There is nothing mysterious about it, just common context.
The GHZ experiment
Greenberger, Horne, and Zeilinger (GHZ)(note 14) has considered the case when
more than two spin-� particles are emitted from a single source with total spin 0. A
corresponding number of Stern-Gerlach apparatuses are situated around the source such
that we can imagine that all particles are detected with either spin up or down relative
to the field direction of each apparatus. If the angles of the fields with respect to an
arbitrarily chosen direction sum to an integral multiple of 180(note o), a "superclassical"
case occurs such that the direction of one of the spins can be predicted with a 100%
accuracy according to quantum mechanics, if all the other spin directions have been
measured.In their original paper GHZ showed for the fourparticle gedanken experiment that the superclassical correlations cannot be produced by a local hidden variable theory. As discussed by Mermin (note 15), this feature is general when the number of particles is greater than 2. For the Bohm-variant of the EPR experiment (or Aspect's) with only 2 particles the superclassical correlation for parallel polarizers conforms with Bell's inequality.
For the case of three particles in a certain state Mermin shows (note 16) that the product of the three measured spin values s1s2s3 (s is +1 for up-spin, and -1 for down) is +1 every time two of the particle spins are measured in the y- direction and the remaining in the x-direction, but if all three spins are measured in the x-direction, the product will be -1. This then means that we can predict the third spin with certainty when we know the values of the first two. Such a correlation could not be produced by a classical model, claimed Zeilinger at the Joensuu Conference. A similar claim had also been put forward by H. Stapp.
In my remark at the discussion of Zeilinger's paper I maintained that classical models of such correlations could easily be made, provided a common experimental context existed for the separate particle detections, a coincidence counter. The next day I presented to Zeilinger a story from Smullyana to prove my point. As Zeilinger's presentation of the case was slightly different from Mermin's, my story was also slightly different from the one below.
The sociology institute has now an investigation going where they study "triple families", consisting of three people. Every such triple is interviewed with its members separated such that they cannot communicate and do not know what questions the other members are asked. The questions are always of the type: "Do you like the letter x (or y)?", and they are to be answered with either "yes" or "no". Every triple family is to be asked either about x to all its members or about x to one of them and about y to the other two.
The institute's staff consists of black men, white men, black women, and white women. For some reason the institute decides that every time the number of y-questions is 2 the interview of the members of a triple family shall be conducted by a woman (black or white) and by a man (black or white) every time this number is zero.
What the sociologists don't know is that every triple family contains exactly one "sexist" and two "racists". A sexist will always answer "yes" to such an innocent question when it is asked by a woman and "no" to a man. A racist will always answer "no" to a black and "yes" to a white.
One can then easily see, that the product of the three answer values (+1 for yes, -1 for no) will have the same value as in the GHZ-three-particle-experiment. Whenever all the questions concern the letter x, they are asked by a male sociologist, so the sexist will answer "no" and the two racists will answer the same, depending on whether he is black or white, so the product is -1. When two of the questions concerns y and the remaining x, and the interviewer is female the sexist answers "yes" and the two racists answer the same, and the product is +1.
Zeilinger remarked to the story that the correlations would not arise if the questions were asked by different people (statistically independent, regarding gender and race) and the answers compared afterwards, and I agree of course. This is just the crucial point: Superclassical correlations or violation of Bell's inequalities may arise within a classical framework in the absence of any non-local effects, but only in a situation where a common context exists for the different questions such that this context in some way reflects the combination of questions.
In real experiments the coincidence counters are the only visible common context for the different particle detections. My conjecture is therefore that an experiment without these central counters (i.e. with individual time records of single-detections and "retrospective" coincidence counting) would conform with Bell's inequalities. If such an experiment is performed and it turns out that the inequalities are broken in the way predicted by quantum mechanics, I would still maintain that there exists a common context like in the examples above, but it would be difficult to point to any specific part of the experimental equipment as providing this contextuality. That would be a real drawback for the comprehensibility of quantum mechanics. As pointed out by Fernandez (note 3) quantum mechanics as developed by Bohr shares with Peirce the faith in the validity in "theorematic reasoning", i.e. logical conclusions based on idealized diagrams of experimental situations. It must be possible for experimentalists to describe the decisive features of their equipment "in classical terms" as Bohr said and by means of icons (diagrams) as Peirce said, such that these icons, instead of the real physical apparatuses, can be used by theoreticians as the basis for drawing inferences. If this principle is not valid, quantum mechanics and the whole of physics will be in serious trouble and the door is wide open for extravagant and unfalsifiable ontological claims (many-worlds).
It is of course a problem to understand how the coincidence counters can make their presence known to the individual particles, because the normal assumption is, that the amplification in the single-detectors act in a way to make the connections to the coincidence counters act as classical one-way-channels. I have elsewhere (note 17) pointed to the quantum mechanical zero-point noise in the dissipative registration devices as described in the fluctuation-dissipation theorem as a sign of consistency for quantum mechanics pointing to the limitation of the formalism in connection with dissipative processes, especially the measuring processes. The description of an idealized measure- ment inherent in the collapse postulate is the semantic basis for quantum mechanics and as such it lies outside the scope of explanation of the simple theory. The conceptual difficulties like Schrödinger's cat and the missing "objectification of the pointer position" described by Mittelstaedt and others at this conference points to the need of a measurement theory that involves something beyond the usual Hilbert space formulation, e.g. an "algebraic quantum mechanics" (Primas), a stochastic dynamic (Ghirardi) or some hidden variables describing the real equipment instead of some mysterious "implicate order" of nature.
However, if it is not possible to understand the basic quantum semantic by theorematic reasoning the whole foundation of the more elaborate theories seems very shaky.
References
- J. Buchler (ed.), Philosophical Writings of Peirce, Dover, N.Y. (1955). (Especially the articles "The Architecture of Theories" (1891), "The Doctrine of Necessity Examined", and "The Law of Mind" (1892)).
- C. Hartshorne, Charles S. Peirce and Quantum Mechanics, Transactions of the Charles S. Peirce Society, 9, 191 - 201 (1973).
- E. Fernandez, From Peirce to Bohr: Theorematic Reasoning and Idealization in Physics. Paper presented at the Charles S. Peirce Sesquicentennial Congress, Harvard, september 1989.
- The New Elements of Mathematics by Charles S. Peirce, ed. Carolyn Eisele, The Hague: Mouton, vol. 1-4 (1976).
- E. Santos, Phys. Letters, A 115, 363 (1986).
- D. Mermin, Physics Today, april 1985. (See also the comments in the issue of november).
- J. F. Clauser and A. Shimony, Rep. Prog. Phys. 41, 1981 (1978).
- A. Fine, Phys. Rev. Letters, 48, 291 (1982).
- A. Shimony, British Journal for the Philosophy of Science, 35, 25 (1984).
- P. V. Christiansen, Proceedings of the 1987 Joensuu Conference, Sympo- sium on the Foundations of Modern Physics, World Scientific, Singapore (1987). (Preprint available as IMFUFA text no. 144.)
- A. Shimony, Proc. Int. Symp. Foundations of Quantum Mechanics Tokyo (1983), pp. 225 - 230.
- A. Aspect and P. Grangier, ibid. pp. 214 - 224.
- R. Smullyan, What is the Name of This Book?, Englewood Cliffs, N.J.: Prentice Hall (1978).
- D. M. Greenberger, M. A. Horne, and A. Zeilinger, in Bell's Theorem, Quantum Theory and Conceptions of the Universe, ed. M. Kafatos, Kluwer Academic Publishers, Dordrecht (1989).
- N. D. Mermin, Phys. Rev. Lett., 65, 1838 (1990).
- N. D. Mermin, Physics Today, 43 (6), 9 (1990).
- P. V. Christiansen, The Semiotics of Quantum-Non-Locality, IMFUFA text no. 93 (1985).