1. The concept of emergence and the Peircean categories
When we try to trace the evolution of the universe forwards from the beginning we seem to encounter an indefinite number of emergent steps. Skipping over the formation of various elementary particles and the lightest atomic nuclei we reach a state where there is still no structure on the macroscopic scale. The whole universe is in a plasma-state of internal equilibrium between matter and radiation, but it is expanding, and its temperature is dropping. About 700.000 years after the Big Bang the plasma has become cooled to a point just below the ionization energy of hydrogen. The stable hydrogen atoms that are subsequently formed are electrically neutral and do not, therefore, interact nearly as strongly with the electromagnetic radiation as their constituent charged particles (electron and proton). The ability of the radiation to keep particles of matter dispersed in the plasma vanishes, and the particles begin to clump together under the influence of their own attractive force of gravitation. In the uniform plasma state gravitation pulls equally in all direction, but if a larger concentration of matter occurs by chance in a certain region there will be a net gravitation force attracting nearby particles towards the center of the collection, and the lump grows and becomes even more attractive. The universe has reached the point of emergence of galaxies, a very crucial point in prebiotic evolution, as also mentioned by Jesper Hoffmeyer.This transition also would have been felt by particles as the emergence of gravitation, because before the occurrence of lumps of matter all gravity canceled out to zero, but suddenly there was an actual force pulling the particles towards the center of a nearby lump. However, gravitation was there all along, because otherwise no lumps could be formed. It had just been slumbering before in a state of potentiality, and now it became actualized. As the seeds of matter aggregation grew and stabilized themselves as galactic collections of dust and stars, gravitation became generalized to act as the dominant force of the large scale universe. The process of generalization can also be described as habit formation: The accidental initial occurrence of a growing seed of matter concentration tends to redistribute all matter of the universe so that similar ocurrencies become less accidental and more predictable in the future.
Instead of using the word emergence as a magic spell, suggesting that suddenly there is something which did not have the slightest existence before, we have here a description of the formation of galaxies as a continuous process of growth and self-organization. The dualistic notion of existence versus non-existence is thus replaced with a notion of three modes of being, the three phenomenological categories of C. S. Peirce (note 1):
- Firstness = the potential.
- Secondness = the actual.
- Thirdness = the general.
The formula for emergence climbing up through the Peircean categories may be stated as follows:
In the beginning there is a chaotic state of Firstness, where virtual seeds of order may arise for a moment and dissolve immediately. However, a process of continuous change of boundary conditions may lead to a state, where an accidentally formed seed may be stable. This actualized seed marks the transition to Secondness, where the real existence of structure still has no generality and no significance. If the seed has the ability to catalyze its own growth under the changed conditions, it wil initiate a habitual forming of similar ordering in its surroundings, and thus the specific type of ordering acquires significance and a state of Thirdness has been obtained.
The formula above is an almost literal rendering of the famous Peirce quotation from "The Architecture of Theories" (1891) (note 2):
"- in the beginning - infinitely remote - there was a chaos of unpersonalized feeling, which being without connection and regularity would properly be without existence. This feeling, sporting here and there in pure arbitrariness, would have started the germ of a generalizing tendency. Its other sportings would be evanescent, but this would have a growing virtue. Thus the tendency to habit would be started; and from this, with the other principles of evolution, all the regulariti- es of the universe would be evolved."The various disciplines of Physics emphasize the Peircean categories in different ways. In Classical Mechanics only Secondness occurs: There is no spontaneity (Firstness) and no irreversible tendencies to seek equilibrium in various types of attractors (Thirdness), only specific states leading to specific trajectories through the state space. In Thermodynamics both other categories enter the scene: Thirdness by the irreversible tendency of the systems to end in an equilibrium state, determined by the boundary conditions, where all features of the initial state have been wiped out by internal friction. Firstness is reflected in thermodynamics by the spontaneous random fluctuations around the mean behavior, conditioned by the temperature and the frictional forces. The Firstness category is the most difficult to grasp, because when we try to exemplify it by specific examples and general types we are already introducing Secondness and Thirdness. However, Firstness has made a remarkable entry into Quantum Mechanics through the concept of the wave function as describing the state of a system. The properties of a system that are inherent in its wave function are only potential, not actual. An electron has no definite position or momentum; these properties only become actualized in the context of specific types of apparatus and acts of measurement.
In the discussion of the evolution of life and its general types and functions it may be argued on Peircean grounds, that Life itself is a potentiality and thus belongs to the category of Firstness. Like gravitation in the example of the nucleation of galaxies it must have been there before its specific and general manifestations, like pieces of RNA and the genetic code. These manifestations did not suddenly occur but must have been preceded by a long process of experimentation and virtual attempts. The emergence of the whole multitude of life-forms and behavioral patterns may thus be regarded as a long process of awakening from a dreaming sort of life. Life, as a Firstness, did not emerge but existed all along with the physical universe from the very beginning. Its general features in the present state, like the code duality (J. Hoffmeyer) must have emerged from Firstness through Secondness to Thirdness.
2. Mean field theory of sponteneous ordering
A simple physical model for the emergence of order is found in the thermodynamic description of phase transitions. In many cases one of the two phases involved possesses af type of order that is absent in the other phase. For example, the liquid phase exhibits a surface, the gaseous phase has none. The ferromagnet has a spontaneous magnetization below the Curie-temperature, but above this temperature it is paramagnetic with no magnetization in the absence of an external magnetic field. The superconductor has a condensate consisting of paired electrons which are not found in the normal metal. The ordered phase of
-brass (50% Cu and 50% Zn) has a long range
order, the Cu-atoms tend to occupy the positions on
one of two interpenetrating crystal lattices and the Zn-
atoms tend to occupy the other lattice, and this long
range order vanishes in the disordered phase (but still,
a short range order prevails). In all these cases it is
possible to describe the type of ordering by introducing
an order parameter, and the transition from the
disordered to the ordered phase in the absence of an
external ordering field is then a so called second
order phase transition, where the order parameter
spontaneously forms as a seed at a certain critical
temperature and grows in a continuous way below this
temperature. The spontaneous formation of order is
associated with a breaking of the symmetry of the
disordered phase, e.g. the magnetization of a
ferromagnetic has a specific direction in space whereas
the paramagnetic phase is isotropic and has no preferred
direction. The choice of a specific direction is totally
random: there is no way it can be predicted from the
properties of the disordered phase.
In cases where the order is induced by the presence
of an external ordering field the transition to the
ordered phase is discontinuous and not spontaneous. In
this case we have a first order phase transition.
The ordering field may be as simple as an external
pressure (in the gas-liquid transition) or a magnetic
field (in the paramagnet-ferromagnet transition), but in
other cases, like superconductors and -brass the
ordering field is of a more subtle nature and may be
difficult to provide from external sources in the
laboratory.
In the so called mean field theory of phase transitions we imagine that the ordering effect of an external field is assisted by an internal field which is created by the induced or spontaneously formed order parameter. The internal field must be locally determined by the locally existing order, and it can therefore be expected to fluctuate wildly from place to place in the disordered phase, but the mean field theory disregards all these fluctuations and consider only the action of an averaged internal field. In this way we get a simple and general theory of all sorts of disorder- order transitions. The mean field approximation works very well in the case of superconductivity and gravitational nucleation (galaxy formation), but in other cases, such as ferromagnets, it gives only a qualitative understanding. However, a qualitative description is all we need in this context, so we shall specialize to the case of the paramagnet- ferromagnet transition.
In the disordered phase (paramagnet) we can use a linear response model for the ordering effect of the fields. A magnetic field H induces a magnetization M, given by:
where KHI is the paramagnetic susceptibility. According to statistical mechanics this can be expressed as
where C is the Curie-constant and T is the absolute temperature. Considering now, that the induced magnetization creates an internal ordering field Hi by some linear relation
and that the effective field in (1) is the sum of the external field He and the internal mean field, Hi, we have a model of linear positive feedback:
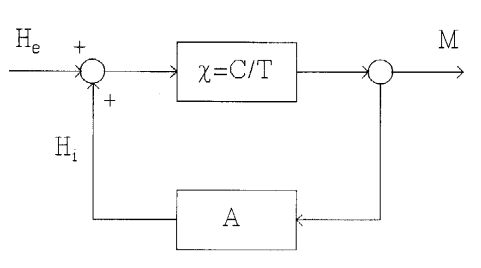
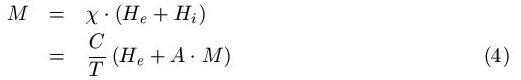
can now be solved for M, and we obtain:
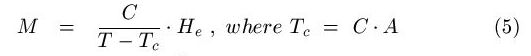
It is seen that the linear feedback model can only be valid for temperatures above the critical temperature (the Curie temperature) Tc. At Tc we may have a finite order parameter M for a vanishing external ordering field. The critical temperature, therefore, marks the onset of instability of the disordered phase.
What happens below the critical temperature the linear feedback model can say nothing about. The actual value of the spontaneously formed and stabilized order parameter is determined by non-linear characteristics of the system. The situation is well known, e.g in an auditorium where a microphone and an amplifier transmits the speaker's words to a loudspeaker. When the amplification is too high (a large value of KHI) or the loudspeaker is too close to the microphone (a large value of A) a screaming noise emerges whose loudness and main frequencies are determined by the non-linearities of the amplifier.
The linear behavior of the system in the disordered phase can be described with a thermodynamic potential that is quadratic in the order parameter:
and the equilibrium value of the order parameter is then the unique value that minimizes the potential, i.e.
Comparing this with eq. (5) we find that 
is given
by:
Following the russian physicist L. D. Landau (1950) (note 3) we now introduce the non-linearity in the simplest possible way by adding a fourth order term to the thermodynamic potential (6):
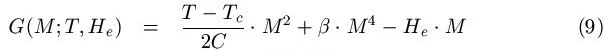
This expression is to be regarded as a series
expansion to the lowest significant order in M in the
neighborhood of the critical temperature. The reason why
the fourth order becomes significant near Tc is
that the second order term vanishes at Tc due to
the feedback mechanism. The coefficient does not
vanish and can therefore be regarded as a constant in
the critical region.
Dependent on the two control parameters T and He the expression (9) will have either one or two minima as a function of the order parameter M. The region with two minima in the control parameter plane is bounded by the curve
This curve, which exhibits a cusp at T = Tc and He = 0 is the catastrophe set, and the Landau mean field theory is thus an example of the cusp catastrophe of René Thom (note 4). In figure 2 the catastrophe set is seen together with three examples of the function G(M), two for points A- and A+ on the catastrophe set and one for the point A0 where the external ordering field is absent and the function has two symmetric minima:
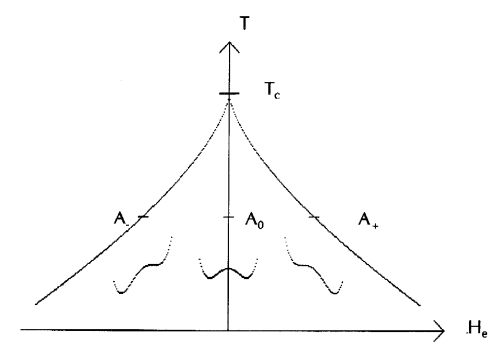
When there is no external ordering field and the temperature is slowly decreased from above to below the critical temperature we get a second order phase transition at the cusp point associated with a spontaneous break of symmetry, a forced choice between the two symmetric minima. The emergence of a new type of order in the universe must happen in a similar way, because the ordering field must be slumbering in a state of Firstness before the order parameter has suggested itself and has grown from its first random seed.
3. The sign relation and the law of mind
The feedback model in figure 1 describes the emergence of order as due to a sort of self reference. The order parameter, whose seed arose by pure chance, refers back to and thereby enhances itself through the action of the internal ordering field. In a similar way a chemical chain of reactions may become significant by autocatalysis when one of the initial reactants occurs as a reaction product later in the chain:
This sort of self reference on a pre-biological stage of the evolution seems to be a necessary condition for the emergence and spreading of symbolic signs, i.e. signs existing on the level of Peircean Thirdness. The internal self reference (autocatalysis) establishes a habit which is the meaning and interpretant of the sign. The habit tends to spread out to the surroundings by cross-catalysis and thus new symbolic signs become associated with the first. The sign is not dependent on a pre-existing consciousness in order to acquire meaning, but meaning is created by the internal awareness of self and others that grows from self reference and associative power (auto- and cross- catalysis). This mechanism of emergence is what Peirce calls The Law of Mind.
The definition of a sign, according to Peirce, ought to be free from reference to human consciousness, or language, although this may seem awkward. (In many cases he includes a human interpreter in the sign definition, but admits that this is a "sop to Cerberus"). The "purest" formulation in this sense (note 5) makes it clear, that self-reference must be inherent in the definition of the sign. Below, we analyze this definition, which for the sake of clarity is here divided into smaller sections:
- A Sign, or Representamen, is a First
- which stands in such a genuine triadic relation to a Second, called its Object,
- as to be capable of determinig a Third, called its Interpretant, to assume the same triadic relation to its Object in which it stands itself to the same object.
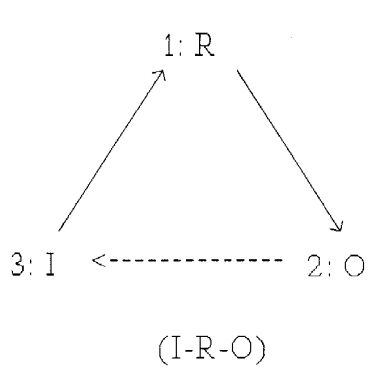
At the bottom of the figure is shown a linear representation of the sign relation, I-R-O with two sign links (-) connecting the three factors, R, O, and I. The sign links represent physical processes and are interaction bonds, i.e. each link contain two oppositely directed causal relations, as can be seen by comparison with the triangular causal diagram above. The linear diagram has the advantage of showing that the causal relation between O and I can only exist as mediated by R. Also, it makes it easier to depict a chain of signs, where the interpretant of the first relation becomes the representamen of the second relation, and the representamen of the first relation becomes the object of the second relation.
The reflexivity of the sign relation is the feature that makes this particular way of chaining signs possible, in a way similar to the way autocatalysis is generalized to cross-catalysis. This is the idea of unlimited semiosis, the potential of creating new meaning that is inherent in Peirce's conception of meaning and in the Law of Mind. In continuation of the sign definition quoted above he says:
"The Third must indeed stand in such a relation, and thus must be capable of determining a Third of its own; but besides that, it must have a second triadic relation in which the Representamen, or rather the relation thereof to its Object, shall be its own (the Third's) Object, and must be capable of determining a Third to this relation. And this must equally be true of the Third's Thirds and so on endlessly; - - "The diagram below shows how the new interpretant (J, the "Third's Third") can be chained to the first relation I-R-O, so we get J-I-R-O where the second relation J-I-R has I as the representamen and R as the object.
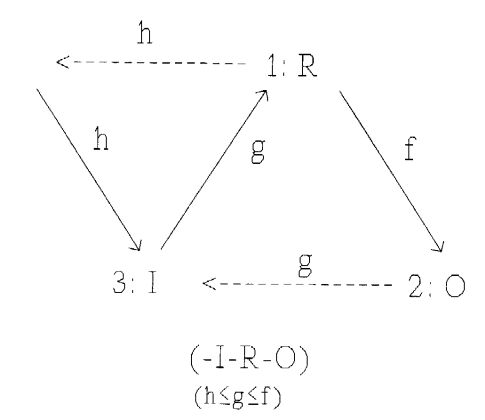
The causal relations in figure 4 are labelled with letters, f, g, and h which have the additional meaning of category numbers assessing the relations as either 1: potential, 2: actual, or 3: general. The following selection rule must be valid in order to ensure that the chain is unbroken:
The links can then be similarly categorized: the R-O link by f, the I-O link by g, because the connection between I and O is established by the I-R link. The g-relations (I-O and I-R) represent the ground of the sign relation (this is not very clearly stated in Peirce's verbal formulations, and there is no general consensus about how "the ground" ought to be defined). The ground (as defined here) and its category number g gives rise to the basic sign classification: 1: icon, 2: index, and 3: symbol. The h-relations and the J-I link is the ground of the second sign relation and categorizes the first relation as 1: rheme, 2: proposition (dicisign), or 3: argument, whereas the category f of the R-O link classifies the representamen as 1: tone (qualisign), 2: token (sinsign), or 3: type (legisign). As the category numbers have to obey the selection rule (11) the more detailed classification based on the triplets (hgf) leads to ten classes of signs that can be arranged in a Pythagorean tetraktys (note 6):
A sign classification scheme like the above represents a sort of evolutionary history of the sign, because a higher category number of a certain link must be built upon the lower categories. Thus the fully developed argument (333) must include all the nine lower classes of the tetraktys and therefore represent a history starting with the qualisign (111) and proceeding by gradually increasing the categories by successive actualizations (1 to 2) and generalizations (2 to 3). Generally, a chain with n links where the category numbers of the links obey the selection rule (5) (i.e. never increasing when going from the object O down the chain to the left) will correspond to the following number of classes:
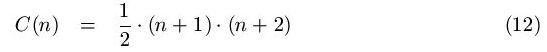
So, the classification of the ground (n=1) gives C(1)=3 classes (icon, index, symbol), the three link description gives C(3)=10 classes. It is then tempting to regard the sign as a ten-link history and go further in the classification to C(10)=66 classes, and this is in fact the number given by Peirce for the next level of classification (note 7).
Returning for a moment to the initial example of matter and gravitation: We can regard a force of gravity as a sign (R) pointing to an object (O) that is a collection of mass. The interpretant (I) is then the general understanding, the recognition of a habit, that is expressed in the law of mass attraction by gravitation. However, this triadic sign relation also contains a history of evolution in three stages: First, the mass was dispersed and its gravitation only potential, but a random collection took place. Second, the lump of matter persisted long enough to be a distinct entity. Third, the gravitational force attracted matter from the surroundings until a habitual balance was obtained. These two descriptions are a synchronic and a diachronic elaboration in three links of the one link ground, gravitation as a sign. A further elaboration will lead to a synchronic classification with ten classes (the tetraktys) and a diachronic history of evolution through ten stages. If a sign is not fully developed to thirdness in all its links, its history will be accordingly truncated, i.e. from some stage its links are not understandable (habitual, general), but only (accidentally) actual or potential.
4. Entropy, information, and meaning
It has been argued in this paper that we may speak of meaningful structures as something that has to do with the formation of habits in the physical universe, i.e. Peicean Thirdness, and that this "Law of Mind" does not presuppose human consciousness. This way of speaking should not be construed as a sort of physical reductionism, but rather as an attempt to show, that even the physical description presupposes some "anthropomorphic" concepts, like "habit" and "choice" that are not derivable from physical first principles. Life, considered as a Peircean Firstness, has been there all the time, but we must try to understand how the present life-forms have emerged in a continuous way from its pre-biotic beginnings.
An alternative approach to the discussion of meaningful structures on a physical basis is the attempt to discuss "information" as something related to physical entropy, as presented by Tom Stonier at this conference. A few critical remarks to this approach may be relevant here.
"Information" may be without any meaning and still exist. "Meaning" is something general, a Thirdness, but a specific string of letters, like "sjxipesdqo" that contains information, does not necessarily contain meaning. From the viewpoint of the telecommunication engineer it is essential that the information transmitted through a telephone line is actual, but meaningless, i.e. it exists on a level of Peircean Secondness. Entropy in a physical system is not "lack of information" i.e. non-existing information, but potential information about the exact microscopic state of the system. In principle this information could be obtained or actualized whereby the microstate would be known and the entropy reduced to zero. In this case the existing information would change its mode of being from firstness to secondness, but thirdness is out of the question, because it is a specific information that cannot be generalized. So, entropy is a potential, meaningless information. If we try to build a theory of meaning by saying that "entropy is lack of information, so information must be negative entropy, and information has meaning", then we are in fact saying that meaning can be understood as "lack of meaninglessness".
There is nothing wrong with Shannon's "Theory of Information" when we remember that the potential meaning of the Shannon-information is outside the scope of the theory and is left to the human listener on the telephone. Also, there is nothing wrong with the information theoretical description of physical entropy as potential information about the microstate of a physical system, so it is not just a funny coincidence that Shannon's information and Gibbs' entropy are given by the same probabilistic formula. The physical information theory, as worked out by Szilard and Brillouin (note 8) in the discussion of Maxwell's demon has something important to say on the physical limits of how much structure a system can exhibit, but it can say nothing about whether these structures are meaningful or not.
A theory of meaning must take departure in the concept of a sign, and here Peirce's semiotic philosophy, physical theories of spontaneous order formation, and Ren� Thom's catastrophe theory are applicable, because they build on the notion of an underlying continuum from which discrete categories may emerge by continuous growth and habit formation. In this way we may be able to bridge the gap between naturalistic and humanistic studies.
References
The abbreviation CP refers to:Collected Papers, C. S. Peirce, 1969, ed. Charles Hartshorne and Paul Weiss, The Belknap Press of Harvard University Press, Cambridge Mass., vol. 1-8.
- J. Buchler, Philosophical Writings of
Peirce, 1955, Dover Publications, Inc.,
New York.
The categories are introduced in the article The Principles of Phenomenology, section 2, which is from a manuscript from 1902 (CP 1.23-6). - The Monist, vol. 1, 1891. See ref. 1 or CP 6.7-34.
- L. D. Landau and E. M. Lifshitz, Statistical Physics, 1959, Pergamon Press, London.
- T. Poston and I. Stewart, Catastrophe Theory and its Applications, 1978, London.
- CP 2.274, ca 1902, or ref. 1, p. 99-100.
- CP 2.243 or ref. 1 p. 115-119.
- Peirce's letter to Lady Welby, december 23.,
1908. See:
I. C. Lieb, Charles S. Peirce's Letters to Lady Welby, 1953, New Haven. - L. Brillouin, Science and Information Theory, 1962, Academic Press, N.Y.