Quantum Semiotic and Interaction Bond Graphs
Peder Voetmann ChristiansenDept. of Mathematics and Physics
Roskilde University
P.O.Box 260, DK 4000 Roskilde, Denmark
fax (+45)46743020, E-mail: pvc@ruc.dk
5 Keywords: Semantics, Peircean Sign Relation, Realism, Ontology
1. (What is the problem to resolve?)
The quantum formalism, although well- established and confirmed, still seems counter-intuitive in many ways. How do we develop our mental images of reality and an epistemological framework such that the whole thing will seem intuitively clear and sensible?
1. the Vicious Circle of Quantum Semantics
"There can be no question of any unambiguous interpretation of the symbols of quantum mechanics other than that embodied in the well-known rules which allow to predict the results to be obtained by a given experimental arrangement described in a totally classical way."This statement of Quantum Semantics leads into a vicious circle for a theory of measurements: How can we know that a given piece of measurement equipment "described in a totally classical way" will behave according to the "well-known rules"? A quantum mechanical account of the action of the apparatus is out of the question because the meaning of the quantum symbols is undefined, unless the classical description alone provides a sufficient guarantee for its proper functioning. The Copenhagen interpretation is thus unable to tackle the measurement problem, except for some vague hints to the Correspondence Principle and an anti-realistic conviction that the reduction or collapse of the wave function is a purely conceptual tool with no physical background.
2. Non-Locality or Contextuality?
It is necessary to break the vicious circle of quantum- semantics such that the setting of semiotic sign- relations by physical means is considered more basic than semantics.
3. Sign relation and Quantum Semiotic.
2. Actuality
3. Generality
The three categories of the two links have to be combined with the selection rule that the category of the Detection (I-R) link (1:icon, 2:index, 3:symbol) cannot exceed the category of the Preparation) (R-O) link (1:tone, 2:token, 3:type). The semiotic classification of the two-link sign then leads to six classes of signs that can be related to the Dirac-notation in the following way:
| (33) symbol 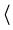 q q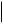 p p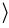 |
|||||||||||||||||
icon-type 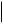 p p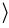 |
index-type 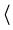 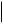 p p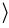 |
||||||||||||||||
tone Hilbert Space H |
icon-token 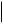 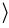 |
index-token 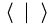 |
|||||||||||||||
4. Interaction Bonds as sign links.
The iconical (pictorial) representation of dynamic relations in the formalism makes it possible to circumvent the prohibition against ontology and the use of mental images of the quantum world. An implementation of the bond-graph icons as computing elements may provide a crucial step in the development of quantum computers. In the most general formulation of the technique every bond is associated with a metric tensor that defines the scalar product of the two complex vectors (effort and flow) that constitute the interaction. The technique thus incorporates the general principle of relativity, including Einstein-locality. The Reticulation (network-structuring by bond- graph-icons) of the sign relation leads for the representamen R to the partial differential wave- equations described as sections repeated in space like a three dimensional crystal. The processes of Preparation and Detection, associated with the R-O, and the I-R bonds, respectively, are naturally Quantized as causal shifts that are distributed through the network from the connecting junctions. In this way the quantization of action and the projection postulate for measurements are given a natural and realistic explanation.
5. References.
- A. Aspect, J. Dalibard, and G. Roger, Phys. Rev. Lett. 49, 1804 (1982).
- G. Weihs, A. Zeilinger, et al. "The EPR Gedankenexperiment in Real World", Preprint, Institut fr Experimentalphysik, Universit„t Innsbruck, (june 24,1998).
- N. Bohr "Can Quantum Mechanical Description of Physical Reality Be Considered Complete", Phys. Rev. 48, 696 (1935).
- P.V. Christiansen, "Peircean Local Realism Does Not Imply Bell's Inequalities", Preprint, Symp. the Foundations of Modern Physics, Joensuu, Finland, 1990.
- A. Shimony."Controllable and uncontrollable Non- Locality", Proc. Int. Symp. Foundations of Quantum Mechanics, Tokyo. (1983).
- C.S. Peirce "the list of Categories: A Second Essay" (1894), Collected Papers (ed. Hartshorne and Weiss, CP 1.300-303.
- H. M. Paynter, Analysis and Design of Engineering
Systems, MIT, Cambridge, MA (1960).
D. Karnopp and R.C. Rosenberg, Analysis and Simulation of Multiport Systems- The Bond Graph Approach to Physics Systems Dynamics, MIT, Cambridge, MA (1968)