Axioms of Quantum Semiotic
Peder Voetmann ChristiansenIMFUFA, RUC
The sign relation
- The quantum mechanical state vector is a sign.
- A sign or representamen (R),
according to Peirce, is a first standing in
such a genuine triadic relation to a second,
called its object (O), as to be capable of
determining a third, called its
interpretant (I), to assume the same triadic
relation to its object in which it stands itself to the
same object.(note 1)
- The representamen R in a quantum semiotic sign
relation mediates between the quantum
mechanical object O and the interpretant I:
I-R-O - The interpretant I is a potential, actual, or general
purely physical result of measurement.
- The sign links ( - ), in the dyadic parts
R-O and I-R of the sign relation are
interaction bonds corresponding to the
physical processes of preparation (the
R-O link) and registration (the I-R link).
- Each sign link is characterized by the Peircean
categories as either 1: potential, 2:
actual, or 3: general.
- The category numbers, f and g,
of the R-O link and the I-R link are restricted by the
selection rule: g
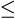 f.
f. - The qualisign 11 (g =
f = 1) is the continuum of the Hilbert
space H. The
symbol (g = f = 3)
is synthesized from the lower signs by
successive actualizations of
potential links (1
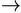 2) and
generalizations of actual links (2
2) and
generalizations of actual links (2
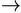 3).
3). - The six classes of signs (gf) are connected
with Peirce's semiotic definitions and Dirac's bra-ket
notation in the following way
(33)
symbol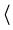 q
q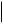 p
p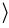
(13)
iconic legisign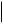 p
p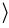
(23)
indexical legisign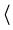
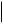 p
p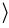
(11)
qualisign
H(12)
iconic sign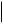
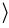
(22)
indexical sinsign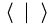
The measurement process
- A measurement is a permanent registration.
The physical setting of an interpretant (the I-R link) preceding the registration is an irreversible process.
- Registration is a dissipative and noisy
process.
- For a dissipative admittance
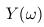 the quantum noise on the
current, whose spectrum is given by the fluctuation-
dissipation (FD) theorem (note 2) corresponds to a time-series of
discrete events
the quantum noise on the
current, whose spectrum is given by the fluctuation-
dissipation (FD) theorem (note 2) corresponds to a time-series of
discrete events
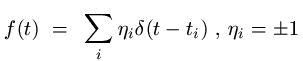
- For a dissipative device with mobility
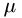 and relaxation time
and relaxation time
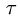 the average number of events up to time t
following an event at time 0 at zero temperature according
to the FD theorem is given by
the average number of events up to time t
following an event at time 0 at zero temperature according
to the FD theorem is given by
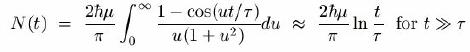
- The collapse or reduction of the state
vector requires the setting of a dissipative sign link
corresponding to the appropriate ray of H
before the measurement. The projection on the
ray is the first of the quantum events predicted by the FD
theorem. (note 3)
- The collapse of a state vector for more than one particle
requires prospective coincidence counting.
- The violation of Bell's inequalities and other superclassical correlations is due to a common context of detection of several particles represented by preset
coincidence counters.
- Quantum Mechanics is strictly local and all the so called "non-local" effects can be simulated in a purely classical and local scenario provided there is a common context for the registration of individuals. (note 4)
Notes:
- Collected Papers, ed. Hartshorne & Weiss, CP 2.274.
- H. B. Callen and T. A. Welton, Phys. Rev., 83, 34 (1951).
- P. V. Christiansen, The Semiotics of Quantum-Non- Locality, IMFUFA text no. 93 (1985).
- See my paper "Peircean local realism does not imply Bell's inequalities", Joensuu 1990.